La gerencia implica tomar decisiones en incertidumbre. Optar por una alternativa (contratar o no a una persona, otorgar o no un crédito, por ejemplo) requiere información precisa y un criterio de elección apropiado, que asegure la mayor capacidad de diferenciación entre las opciones.

Jenifer María Campos Silva / 3 de mayo de 2021

Una herramienta estadística útil para la labor gerencial, porque ayuda a establecer umbrales de decisión apropiados, se conoce como curva de Característica Operativa del Receptor (ROC, por sus siglas en inglés). Una curva ROC permite establecer la capacidad de discriminación de una prueba de clasificación dicotómica (que admite solo dos respuestas posibles): presencia o ausencia de la variable de interés (Del Valle, 2017). Por ejemplo, en una decisión típica del ámbito de recursos humanos, la variable de interés pudiese ser “contratado” o “no contratado”.

La capacidad de diferenciación de una prueba se ve afectada directamente por el criterio discriminante, comúnmente conocido como valor umbral. Este valor puede ser elegido por el decisor de forma arbitraria; pero, de ese modo, no es posible medir de forma adecuada la cantidad de errores que se cometen —y, por lo tanto, no es posible corregirlos— ni comparar una prueba con otras. De allí la pertinencia de la curva ROC, pues permite elegir el mejor valor umbral para una prueba y minimizar los errores cometidos por una mala (incorrecta) clasificación.

Origen de las curvas ROC

Las curvas ROC se derivan de la teoría de la detección de señales, y sus inicios se remontan al año 1941, cuando la Armada Imperial Japonesa atacó Pearl Harbor el 7 de diciembre. Luego del ataque, los ingenieros militares estadounidenses evaluaron de forma más precisa las señales detectadas por los radares, a fin de diferenciar entre una señal de ruido (completamente inofensiva) y una señal de torpedo (que podría ser mortal).

Los radares son dispositivos de detección de objetos que, mediante la emisión de ondas, son capaces de revelar la presencia de objetos en una determinada posición y la distancia a la que se encuentran. Pero los radares de esa época no eran capaces de diferenciar entre las distintas señales recibidas.

Si los parámetros de decisión fueran muy exigentes, prácticamente, ninguna señal sería considerada de torpedo y no se cumpliría el objetivo del radar, que es ayudar a los militares a prepararse para un ataque. Mientras que si los criterios fueran demasiado laxos, con seguridad todos los torpedos serían detectados, pero muchas señales de ruido serían consideradas de torpedo, lo que llevaría a las fuerzas militares a tomar medidas innecesarias de defensa o ataque, y ocasionaría agotamiento y pérdida de recursos.

Ninguna de estas situaciones es ideal. En este caso, el uso de las curvas ROC aportó una solución: determinar valores de sensibilidad y especificidad, las tasas esperadas de falsos negativos y falsos positivos, y cuál de los dos errores era menos costoso (Del Valle, 2017).

Características de una curva ROC

La curva ROC se representa en el primer cuadrante de un plano cartesiano: los valores horizontales y verticales se ubican entre cero y uno, porque consisten en probabilidades. Se suele agregar una diagonal que parte del origen de las coordenadas, punto (0,0), y llega hasta el punto (1,1), que sirve como guía o ayuda visual de la bondad de la prueba discriminante.

El eje vertical se define como sensibilidad de la prueba: la proporción de objetos que presentan la característica de interés (la prueba indica que pertenecen al grupo con esa característica). El eje horizontal se define como el complemento de la especificidad de la prueba (viene dado por la fórmula 1 – especificidad): la proporción de objetos que no presentan la característica de interés (son clasificados en el grupo que no posee la característica) (Del Valle, 2017). En otras palabras, la sensibilidad mide los verdaderos positivos; y la especificidad, los verdaderos negativos.

Suponga una curva ROC formada a partir de un modelo predictivo de la insolvencia de personas naturales en una entidad bancaria. Se puede definir como valor umbral una sensibilidad de 0,8 que daría lugar a un valor de 1- especificidad de 0,24. Esto significa que el 80 por ciento de los casos de insolvencia serían clasificados correctamente; y el 24 por ciento de los individuos que no caerían en insolvencia serían clasificados de forma incorrecta. La pregunta que cabe hacerse es si dicha tasa de error es aceptable, si el modelo permite elegir de manera más precisa. Para ello se debe ubicar un punto sobre la curva y estudiar su sensibilidad y especificidad. Es posible, entonces, encontrar falsos positivos y falsos negativos: objetos mal clasificados por la prueba discriminante.

Una curva ROC hipotética

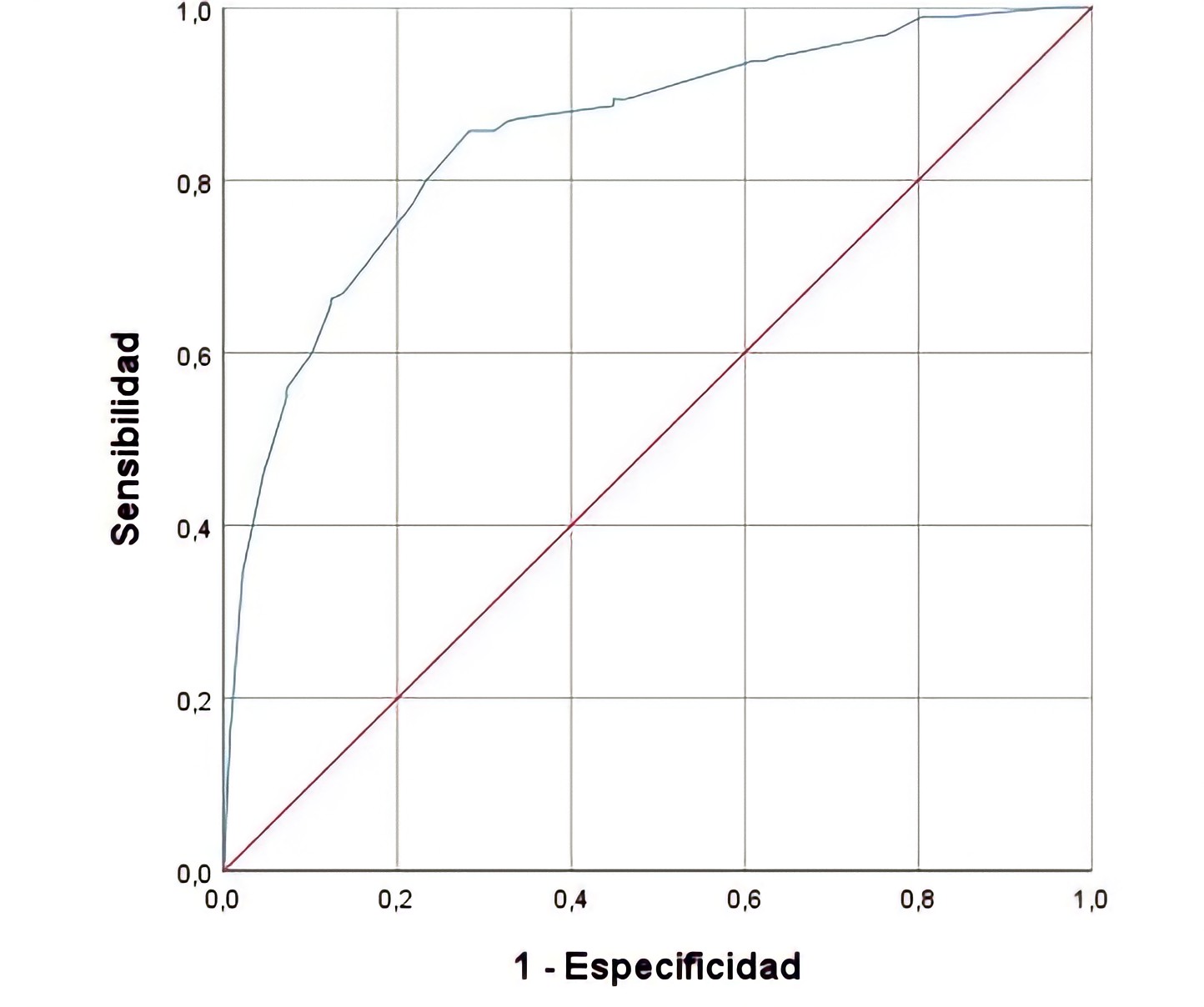
Nota: la línea roja (diagonal) indica una clasificación aleatoria.

Los falsos positivos son objetos que no presentan la característica de interés, pero son clasificados por la prueba en el grupo de los que sí la tienen; por ejemplo, personas que son contratadas sin contar verdaderamente con las competencias necesarias para el cargo. Mientras que entre los falsos negativos se encuentran individuos que teniendo la característica de interés son clasificados por la prueba en el grupo de los que no la poseen.

El éxito de la predicción depende de la ubicación del criterio de decisión; es decir, el valor umbral. Si se establece una alta probabilidad para ser clasificado en un grupo, mejorará la tasa de verdaderos negativos, pero aumentará también la de falsos negativos, pues la exigencia es mayor. Mientras que, si se exige una baja probabilidad para ser asignado a un grupo, aumentarán las tasas de verdaderos y falsos positivos (Meyers y otros, 2013).

La predicción no es perfecta. En cada elección ocurren aciertos y desaciertos; o, en otras palabras, ganancias y pérdidas. Un criterio de clasificación puede consistir en tomar como punto de corte un valor intermedio (0,5) de probabilidad. Así, el punto de corte estaría exactamente sobre la línea diagonal. El problema con este valor umbral es que no se diferencia de un modelo aleatorio (Tufféry, 2011): la decisión se deja al azar.

La principal ventaja de las curvas ROC es que permiten minimizar los falsos positivos y negativos, al clasificar objetos en uno de dos grupos. Además, permiten decidir cuál de los dos errores ocurrirá en menor medida.

Las curvas ROC permiten también comparar modelos de diferente naturaleza, aun cuando sus indicadores de desempeño no sean directamente comparables, y hacer contrastes de alcance local y global; por ejemplo, un modelo puede ser globalmente superior a otro que funciona mejor para discriminar en una población local (Tufféry, 2011).

Las curvas ROC pueden distinguirse por su grado de convexidad: A) poca convexidad significa un área pequeña entre la diagonal y la curva, lo cual indica que el modelo es deficiente; B) un área mayor entre la diagonal y la curva indica un modelo de decisión mejor; y C) la mejor curva presenta un área mayor, su crecimiento es muy rápido al inicio y comienza a ser casi horizontal en valores altos de sensibilidad, lo que permite elegir un mejor valor umbral.

Curvas ROC con distintos grados de convexidad

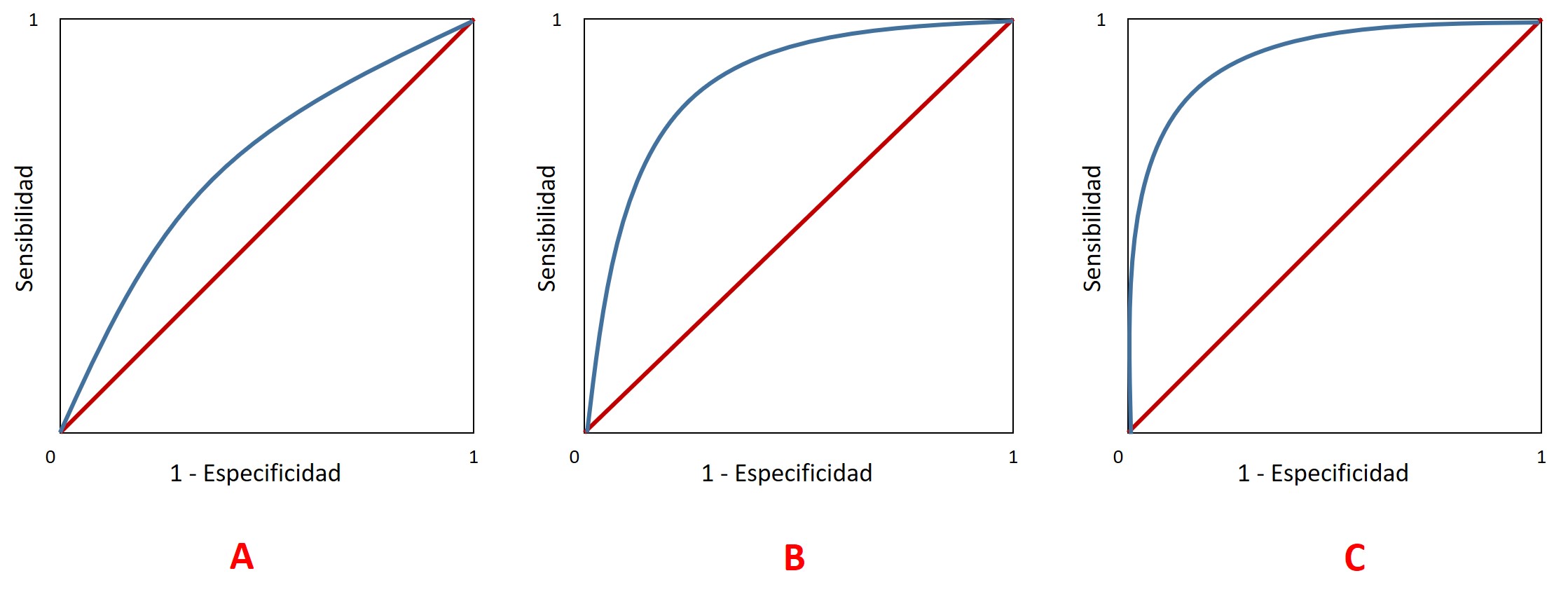
Los mejores criterios de decisión muestran valores altos en el eje vertical (sensibilidad) y bajos en el horizontal (1 – especificidad). Esto asegura altas tasas de verdaderos positivos combinadas con bajas tasas de falsos negativos, lo cual se traduce en bajas tasas de clasificaciones falsas positivas y altas tasas de clasificaciones verdaderas negativas. Estos valores se encuentran cuando la curva ROC está por encima de la diagonal y presenta convexidad: aumenta el área que separa a ambas líneas y, en consecuencia, se separa el criterio de decisión de la posibilidad de que la clasificación sea completamente aleatoria.

Ejemplos de aplicaciones de curvas ROC

Tarapuez y otros (2018) utilizaron una curva ROC para explicar la intención empresarial (IE) de estudiantes de Maestría en Administración en Colombia, y relacionarla con aspectos tales como género, presencia de amigos empresarios, experiencia laboral y edad, que fueron las variables predictivas del estudio. El área encontrada bajo la curva ROC fue interpretada como la probabilidad de que la prueba —basada en las variables predictivas— clasificara correctamente a dos individuos: uno con IE y otro sin IE. El modelo elaborado fue capaz de diferenciar los individuos en un 69 por ciento de las oportunidades, a partir de los factores demográficos mencionados.

También se han elaborado modelos predictivos para aumentar la probabilidad de contacto telefónico efectivo en la gestión de cobranzas. En un estudio realizado en Ecuador consideraron variables de comportamiento crediticio, gestión telefónica, contrato de crédito y demográficas, que permitieron encontrar los mejores horarios de llamada (Uquillas-Andrade y Carrera, 2018). Los resultados indican una buena capacidad de discriminación entre horarios y el mejor resultó 7:00-9:00, seguido por 13:00-16:00. El área bajo la curva ROC fue superior a 0,7.

Otro uso probado de las curvas ROC se encuentra en la minería de datos aplicada a las calificaciones crediticias (Figueroa, 2006). Una actividad frecuente de las entidades bancarias consiste en otorgar créditos a personas naturales y jurídicas, con la expectativa de que devuelvan el dinero prestado más los intereses, que constituyen la ganancia del prestamista. Las entidades bancarias cuentan con modelos que las ayudan a tomar la difícil decisión de otorgar o negar un crédito, con base en la esperanza de que la persona sea capaz de cumplir el compromiso adquirido. Las curvas ROC proporcionan la forma más eficiente de evaluar estos modelos, pues permiten determinar la cantidad de errores que se cometen en la selección y, de esta forma, calcular las pérdidas y ganancias asociadas a las líneas de crédito. La curva ROC asociada al modelo de clasificación se diferencia notablemente de una clasificación al azar, pues indica la bondad del modelo hallado, aunque se aclara que ningún modelo es perfecto.

Jenifer María Campos Silva, profesora del IESA.

Referencias

• Del Valle Benavides, A. R. (2017). Curvas ROC (Receiver-Operating-Characteristic) y sus aplicaciones. Trabajo de grado para la licenciatura en Matemática. Universidad de Sevilla, Departamento de Estadística e Investigación Operativa. https://idus.us.es/bitstream/handle/11441/63201/Valle%20Benavides%20Ana%20Roc%c3%ado%20del%20TFG.pdf?sequence=1&isAllowed=y
• Figueroa, M. (2006). Minería de datos aplicada a credit scoring. Trabajo de grado para la maestría en Matemáticas Aplicadas. Universidad San Francisco de Quito. http://192.188.53.14/bitstream/23000/547/1/82579.pdf
• Meyers, L., Gamst, G. y Guarino, A. (2013). Performing data analysis using IBM SPSS.
• Tarapuez-Chamorro, E., Aristizábal-Tamayo, J. M. y Monard-Blandón, C. (2018). Aspectos sociodemográficos y familiares e intención empresarial en estudiantes de maestría en administración en Colombia. Estudios Gerenciales, 34(149), 422-434. http://dx.doi.org/10.18046/j.estger.2018.149.2757
• Tufféry, S. (2011). Data mining and statistics for decision making.
• Uquillas-Andrade, A. y Carrera, A. (2018). Optimización de contactos telefónicos efectivos en gestión de cobranzas mediante un modelo de mejor horario de llamada, usando regresión multinomial. Maskana, 9(1), 89-103. https://doi.org/10.18537/mskn.09.01.09